爷爷的预测分数

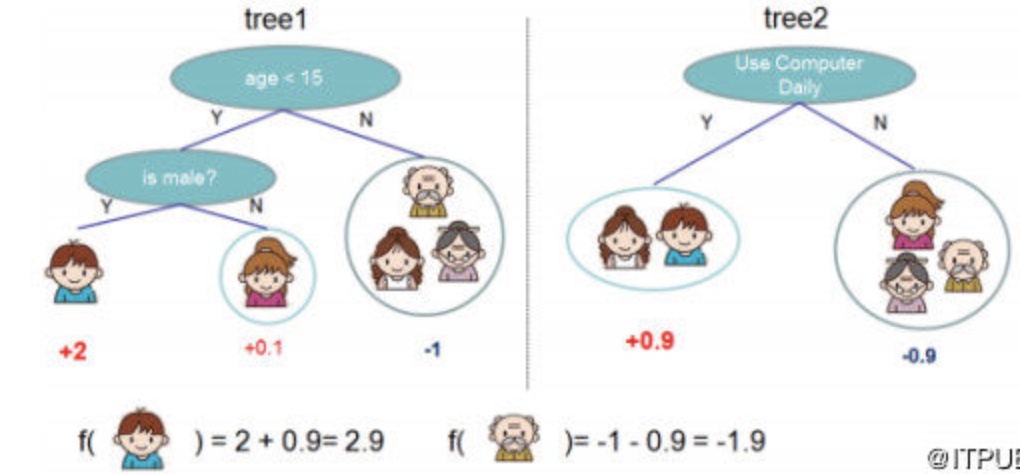
XGBoost考虑正则化项，目标函数定义如下:

很显然,

其中

正如上文所说，新生成的树是要拟合上次预测的残差的，即当生成t棵树后，预测分数可以写成:

同时，可以将目标函数改写成(其中

很明显，我们接下来就是要去找到一个展开近似它。所以，目标函数近似为：

其中

为什么此处可以用二阶导呢?

首先我们需要明确一个概念, 我们的boosting每一轮迭代是在优化什么呢? 换句话说我们在用损失函数

有没有感觉这个公式形式很熟悉, 是不是就是一般常见的linear regression 的 stochastic 梯度更新公式。既然GBDT用的是Stochastic Gradient Descent, 我们回想一下, 是不是还有别的梯度更新的方式, 这时, 牛顿法 Newton's method就出现了。可以说, XGBoost是用了牛顿法进行的梯度更新。

我们先来看一下泰勒展开式:

而对于上面这个公式值, 其与

我们保留二阶泰勒展开:

这个式子是成立的, 当且仅当

即得到:

所以得出迭代公式:

将损失函数与

所以实际上 x 即为 ，故根据二阶泰勒展开,

用替代上式中的, 即可得到 (此处的

这里有必要再明确一下，

我们来看一个具体的例子，假设我们正在优化第11棵CART树，也就是说前10棵 CART树已经确定了。这10棵树对样本

在类别标签时,

我们可以求出这个损失函数对于

将

那么在优化第t棵树时，有多少个

再总结一下,

不过此处所说的不依赖于损失函数形式, 意思不是说在自定义损失函数的时候, 给xgboost传入一个损失函数, xgboost就会自动计算其一阶和二阶导。相反的, 一阶二阶导和 损失函数之间其实算是独立的。XGBoost在每次并行计算的时候独立调用损失函数和一阶二阶导。

我们来看一下python接口自定义损失函数调用XGBoost的方式(代码地址https://github.com/dmlc/xgboost/blob/master/demo/guide-python/custom_objective.py):

#coding:utf-8
import numpy as np
import xgboost as xgb

print('start running example to used customized objective function')

dtrain = xgb.DMatrix('../data/agaricus.txt.train')
dtest = xgb.DMatrix('../data/agaricus.txt.test')

param = {'max_depth': 2, 'eta': 1, 'silent': 1}
watchlist = [(dtest, 'eval'), (dtrain, 'train')]
num_round = 2

#下面这部分就是自定义损失函数, 可以看到, 函数接收两个向量, 一个是预测值pred, 一个是训练数据, 训练数据中包含标签值。在这个函数中, 计算了当前预测值和标签值的损失函数的一阶梯度和二阶导, 并将计算结果返回
#可以看出, 返回的是一阶导和二阶导, 二阶导相当于是Hessian矩阵, 所以此处用了hess作为变量名。很显然, 既然这么设计函数的话, logregobj是可以并行的, 只要每个并行的程序自己调用logregobj即可, 他们之间完全可以互不影响。
def logregobj(preds, dtrain):
    labels = dtrain.get_label()
    preds = 1.0 / (1.0 + np.exp(-preds))
    grad = preds - labels
    hess = preds * (1.0 - preds)
    return grad, hess

#在上面定义完一阶导和二阶导后, 我们此时要计算损失函数, 需要注意的是, 上面的一阶导和二阶导都是矩阵形式的, 不过此处的损失函数的返回值需要是单一的值, 又可称作margin值。回想一下树形结构的公式, 在每个分裂的节点, 该叶节点都对应一个值, 这个值是落在这个叶节点下所有样本的综合值。
def evalerror(preds, dtrain):
    labels = dtrain.get_label()
    # return a pair metric_name, result. The metric name must not contain a colon (:) or a space
    # since preds are margin(before logistic transformation, cutoff at 0)
    return 'my-error', float(sum(labels != (preds > 0.0))) / len(labels)

# training with customized objective, we can also do step by step training
# simply look at xgboost.py's implementation of train
#在obj中传入返回一阶二阶导的函数, 在feval中传入损失函数。
bst = xgb.train(param, dtrain, num_round, watchlist, obj=logregobj, feval=evalerror)

我们回到之前的公式推导环节, 我们已经理解了一阶二阶导, 现在来看正则化项:

其实正则为什么可以控制模型复杂度呢？有很多角度可以看这个问题，最直观就是，我们为了使得目标函数最小，自然正则项也要小，正则项要小，叶子节点个数T要小(叶子节点个数少，树就简单)。

而为什么要对叶子节点的值进行L2正则，这个可以参考一下LR里面进行正则的原因，简单的说就是(对此困惑的话可以跑一个不带正则的LR，每次出来的权重w都不一样，但是loss都是一样的，加了L2正则后，每次得到的w都是一样的)

由于前t-1棵树的预测分数与y的残差对目标函数优化不影响, 可以直接去掉, 所以有:

上式是将每个样本的损失函数值加起来，我们知道，每个样本都最终会落到一个叶子结点中，所以我们可以将所有同一个叶子结点的样本重组起来，过程如下:

因为XGBoost的基本框架是boosting, 也就是一棵树接着一棵树的形式, 所以此处的

因此通过上式的改写，我们可以将目标函数改写成关于叶子结点分数w的一个一元二次函数，求解最优的w和目标函数值就变得很简单了，直接使用顶点公式即可。因此，(还记得上面推导出来的牛顿法吗):

当w取上式最优解时, 之前

我们花了这么大的功夫，得到了叶子结点取值的表达式。在xgboost里，叶子节点取值的表达式很简洁，推导起来也比GBDT的要简便许多。

到这里，我们一直都是在围绕目标函数进行分析，这个到底是为什么呢？这个主要是为了后面我们寻找

具体来说，我们回忆一下建树的时候需要做什么，。比如在详解GBDT里，我们可以选择MSE，MAE来评价我们的分裂的质量，但是，我们所选择的分裂准则似乎不总是和我们的损失函数有关，因为这种选择是启发式的。
比如，在分类任务里面，损失函数可以选择logloss，分裂准确选择MSE，这样看来，。

但是，，这个也是xgboost和GBDT一个很不一样的地方。

具体来说，xgboost选择这个准则，计算增益Gain (其中

其实选择这个作为准则的原因很简单也很直观。 我们这样考虑。由上面的(1)式知道，对于一个结点，假设我们不分裂的话, 那么对于左叶子节点和右叶子节点而言其包含样本点的一阶二阶导的和就不是单独来算了, 而是合在一起。

因为此时所有样本都存在于未分裂的节点中, 所以此时该节点中一阶导的和就相当于

假设在这个节点分裂的话，分裂之后左右叶子节点的损失分别为:

既然要分裂的时候，我们当然是选择分裂成左右子节点后，损失减少的最多(或者看回(1)式，由于前面的负号，所以欲求(1)的最小值，其实就是求(2)的最大值), 也就是找到一种分裂有:

那么

最后就是如何得到左右子节点的样本集合？这个和普通的树一样，都是通过遍历特征所有取值，逐个尝试。

至此，我们把xgboost的基本原理阐述了一遍。我们总结一下，其实就是做了以下几件事情。

1.在损失函数的基础上加入了正则项。
2.对目标函数进行二阶泰勒展开。
3.利用推导得到的表达式作为分裂准则, 来构建每一颗树。

手动还原XGBoost实例过程

下面这个例子由https://blog.csdn.net/qq_22238533/article/details/79477547给出。

上面，我只是简单的阐述整个流程，有一些细节的地方可能都说的不太清楚，我以一个简单的UCI数据集，一步一步的演算整个xgboost的过程。数据集如下:

这里为了简单起见，树的深度设置为3(max_depth=3)，树的颗数设置为2(num_boost_round=2),学习率为0.1(eta=0.1)。另外再设置两个正则的参数,
损失函数选择logloss。
由于后面需要用到logloss的一阶导数以及二阶导数，这里先简单推导一下:

两边对

在一阶导的基础上再求一次可得二阶导(其实就是sigmod函数求导):

所以样本的一阶导数值为:

二阶导数值为:

下面就是xgboost利用上面的参数拟合这个数据集的过程:

建树的时候从根节点开始(Top-down greedy)，在根节点上的样本有ID1～ID15。那么回顾xgboost的算法流程，我们需要在根节点处进行分裂，分裂的时候需要计算之前的式子(2), 即如下:

那么式子(2)表达是：在结点处把样本分成左子结点和右子结点两个集合。分别求两个集合的，然后计算增益Gain。

而这里，我其实可以先计算每个样本的一阶导数值和二阶导数值，即按照式子(3)和(4)计算，但是这里你可能碰到了一个问题，那就是第一颗树的时候每个样本的预测的概率 。具体来说就是参数base_score。（其默认值是0.5）

(值得注意的是，可以理解为一个概率值，提这个原因是后面建第二颗树会用到，需要注意这个细节）

这里我们也设base_score=0.5。然后我们就可以计算每个样本的一阶导数值和二阶导数值了。具体如下表:

一阶导和二阶导

比如说对于ID=1样本, 由上面得到的一阶二阶导公式(3)(4)可得:

那么把样本如何分成两个集合呢？这里就是上面说到的选取一个最佳的特征以及分裂点使得Gain最大。
比如说对于特征x1，一共有[1,2,3,6,7,8,9,10]8种取值(注意上表的ID不代表取值)。可以得到以下这么多划分方式。

1)以1为划分时
左子节点包含的样本:
右子节点包含的样本:
那么左子节点为空，
右子节点的一阶导数和:
右子节点的二阶导数和:
最后我们在计算一下增益Gain，可以有得到Gain=0。
计算出来发现Gain=0,不用惊讶,因为左子结点为空，也就是这次分裂把全部样本都归到右子结点，这个和没分裂有啥区别？所以，分裂的时候每个结点至少有一个样本。

2)以2为划分时
左子节点包含的样本:
右子节点包含的样本:
左子节点的一阶导数和:
左子节点的二阶导数和:
右子节点的一阶导数和:
右子节点的二阶导数和:

3)以3为划分时

上一篇：iOS10 语音识别详解

下一篇：dnssd_clientstub ConnectToServer: connect()-> No o